Ich dachte mir, es wäre mal wieder ganz nett, mal über mein Mathematikstudium (Bachelor) an der FernUni Hagen zu berichten. Geht neben dem normalen Job etwas schleppend voran, aber ein paar Resultate habe ich vorzuweisen – vielleicht kann die ein Mathematiker abseits der Professorenschaft ja mal kommentieren? Bin ich da auf einem guten Weg?
Seminar: Computergrafik
In diesem Seminar wurden jeweils aktuelle, mathematische Forschungsartikel aus dem Bereich Computergrafik verteilt, in deren Thematik wir uns eigenständig einarbeiten mussten. Die Inhalte galt es dann, in angemessener Weise vorzustellen.
Ich erhielt den Text Cross Dissolve Without Cross Fade: Preserving Contrast, Color and Salience in Image Compositing, der sich damit beschäftigt, wie man beim Mischen von Bildern vermeiden kann, dass es zu Verlust von Farbintensität, Kontrast und Elementen mit hohem Informationsgehalt für Menschen kommt. Um das auszuprobieren, habe ich neben der Seminararbeit (Rohformat als TEX-Datei)die Algorithmen für Farbintensität und Kontrast auch in einem Programm umgesetzt. Beispiel gefällig?

Bewahrung der Farbintensität
Auf dem linken Bild sieht man zwei Einzelbilder, die einfach linear interpoliert übereinandergeblendet wurden, jeweils zu gleichen Anteilen. Das rechte Bild zeigt das Ergebnis, wenn man den intensitätswahrenden Algorithmus benutzt. Man sieht das sehr schön am Rot des Würfels.
Das Bild der Würfel stammt übrigens von Ed Sanders und ist verfügbar unter der Creative Commons-Lizenz Namensnennung-Weitergabe unter gleichen Bedingungen 3.0 Unported.
Seminar: Mathematik und Politik
Angenommen, in einem Parlament wären 100 Sitze zu verteilen und sechs Parteien hätten bei der Wahl die folgenden Stimmanteile errungen: A (32,1%), B (28,9%), C (14,3%), D (12,2%), E (8,7%), F (3,8%). Es stellt sich nun die Frage, wie viele Sitze im Parlament jede Partei erhalten soll. Da sich Sitze nicht so einfach teilen lassen, wirft das Probleme auf, die ganz unterschiedlich angegangen werden können.
Meine Aufgabe war es, verschiedene Methoden zur Ermittlung der Sitzverteilung vorzustellen und ihre Eigenschaften zu untersuchen. Meine Seminararbeit dazu trägt den schlichten Titel: Sitzverteilungen (Rohformat als TEX-Datei)
Mathematisches Praktikum unter Benutzung mathematischer Softwarepakete
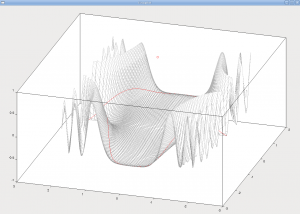
Weg eines Lichtstrahls auf einer Oberfläche
Man stelle sich vor, in einem karthesischen Koordinatensystem sei bei den Koordinaten 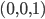 eine punktförmige Lichtquelle angebracht, die eine Oberfläche beleucht. Der Lichtstrahl drehe dabei im Neigungswinkel
eine punktförmige Lichtquelle angebracht, die eine Oberfläche beleucht. Der Lichtstrahl drehe dabei im Neigungswinkel 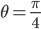 zur „Horizontalen“ um die vertikale Achse, die durch
zur „Horizontalen“ um die vertikale Achse, die durch 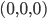 und
und 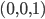 verläuft. Dabei lege er den Winkel
verläuft. Dabei lege er den Winkel 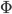 zurück und beschreibe schließlich im
zurück und beschreibe schließlich im 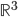 eine geschlossene Kurve.
eine geschlossene Kurve.
Sei nun die Oberfläche durch die Funktion 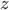 mit
mit 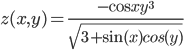 repräsentiert. Meine Aufgabe war es, die Kurve graphisch mittels Matlab darzustellen (habe alternativ das weitgehend kompatible Octave benutzt). Dabei musste ich einerseits die Koordinatenprojektionen der Kurve skizzieren, andererseits überprüfen, ob die Kurve tatsächlich auf der Oberfläche liegt – optisch in einer 3D-Darstellung oder numerisch. Außerdem sollte eine vorgegebene Funktion (bisect) verwendet und die Lösung auf maximal zwei Seiten beschrieben werden: Meine bescheidene Lösung – Liebe Kommilitonen, die ihr euch die Lösung hier abholt statt selbst zu denken (Suchbegriffe sprechen Bände): hinterlasst doch bitte wenigstens einen anonymen Danke-Kommentar.
repräsentiert. Meine Aufgabe war es, die Kurve graphisch mittels Matlab darzustellen (habe alternativ das weitgehend kompatible Octave benutzt). Dabei musste ich einerseits die Koordinatenprojektionen der Kurve skizzieren, andererseits überprüfen, ob die Kurve tatsächlich auf der Oberfläche liegt – optisch in einer 3D-Darstellung oder numerisch. Außerdem sollte eine vorgegebene Funktion (bisect) verwendet und die Lösung auf maximal zwei Seiten beschrieben werden: Meine bescheidene Lösung – Liebe Kommilitonen, die ihr euch die Lösung hier abholt statt selbst zu denken (Suchbegriffe sprechen Bände): hinterlasst doch bitte wenigstens einen anonymen Danke-Kommentar.



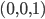 eine punktförmige Lichtquelle angebracht, die eine Oberfläche beleucht. Der Lichtstrahl drehe dabei im Neigungswinkel
eine punktförmige Lichtquelle angebracht, die eine Oberfläche beleucht. Der Lichtstrahl drehe dabei im Neigungswinkel 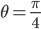 zur „Horizontalen“ um die vertikale Achse, die durch
zur „Horizontalen“ um die vertikale Achse, die durch 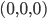 und
und 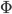 zurück und beschreibe schließlich im
zurück und beschreibe schließlich im 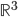 eine geschlossene Kurve.
eine geschlossene Kurve.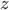 mit
mit 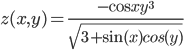 repräsentiert. Meine Aufgabe war es, die Kurve graphisch mittels
repräsentiert. Meine Aufgabe war es, die Kurve graphisch mittels 